Fundamental Concepts Underlying Elliptic Curves (Level 0): High-level Overview

Elliptic Curve is one of the biggest topic in mathematics, for example number theory and geometry, and is used to, for example, proof the famous Fermat’s Last Theorem. It also spawns elliptic curve cryptography, which is widely-used. Understanding elliptic curve can be as simple as taking the rules for granted, but the underlying mathematics is quite complex. We shall have a look at the basic concepts of elliptic curve.

Prerequisites: The definition of a group

2021-12-16: Added some more example code

Introduction

To start out, we can first state what is an elliptic curve on a easy-to-understand form: An elliptic curve over a field \(K\), denoted \(E(K)\), is the set of solutions to the equation \[y^2 + a_1xy+a_3y = x^3 + a_2x^2 + a_4x + a_6\] Where \((x,y)\) are both in \(K\), along with a distinguished point at infinity, usually denoted \(\infty\) or \(\mathcal{O}\).

If the characteristic of \(K\) is not 2 or 3 (for example \(\mathbb{R},\mathbb{C}\), \(\mathbb{Z}_p\) with \(p\) prime and larger than 3 (note we shall use \(\mathbb{Z}_p\) to denote the field \(\mathbb{Z}/p\mathbb{Z}\))), then we can simplify the equation using some coordinate transformations to get a much simpler equation of the form\[ y^2=x^3+Ax+B \] This is called the Weierstrass form. For simplicity we shall consider the Weierstrass form in the following posts.

If the coefficients of the elliptic curve is in a field \(L\), then we say that the curve is defined over \(L\). For example, the curve \(y^2=x^3-x+1\) is defined over \(\mathbb{Q}\). We can consider the solution of the elliptic curve where the coordinates are in \(\mathbb{Q}\), but also it’s extensions like \(\bar{\mathbb{Q}}\) (the field of algebraic integers), \(\mathbb{R}\) and \(\mathbb{C}\) (which is the algebraic closure of \(\mathbb{R}\)).¹

We can graph elliptic curves defined over \(\mathbb{R}\) in \(\mathbb{R}^2\) and it can look like this:

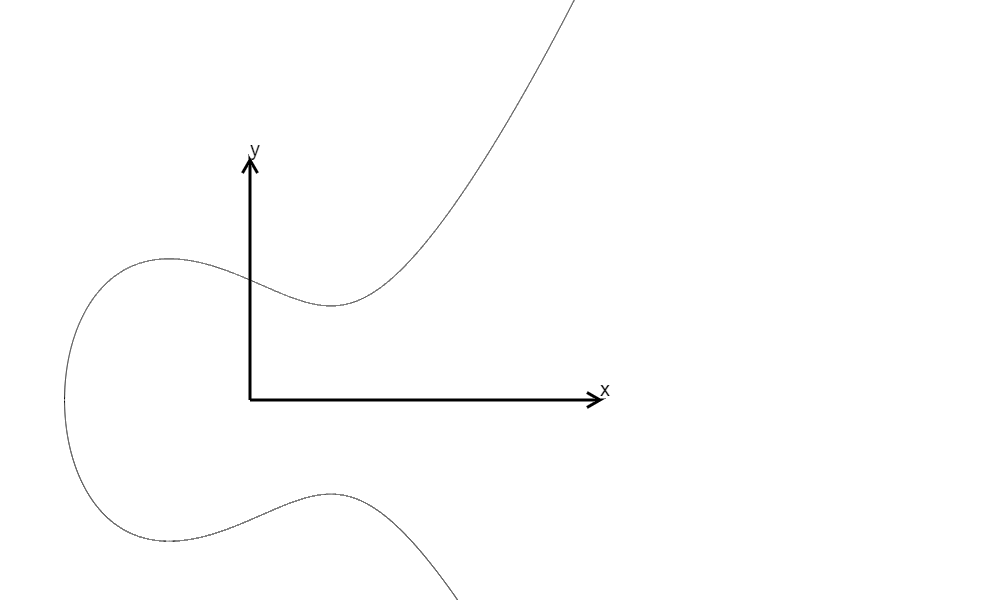\(y^2=x^3-x+1,\Delta=-368\)

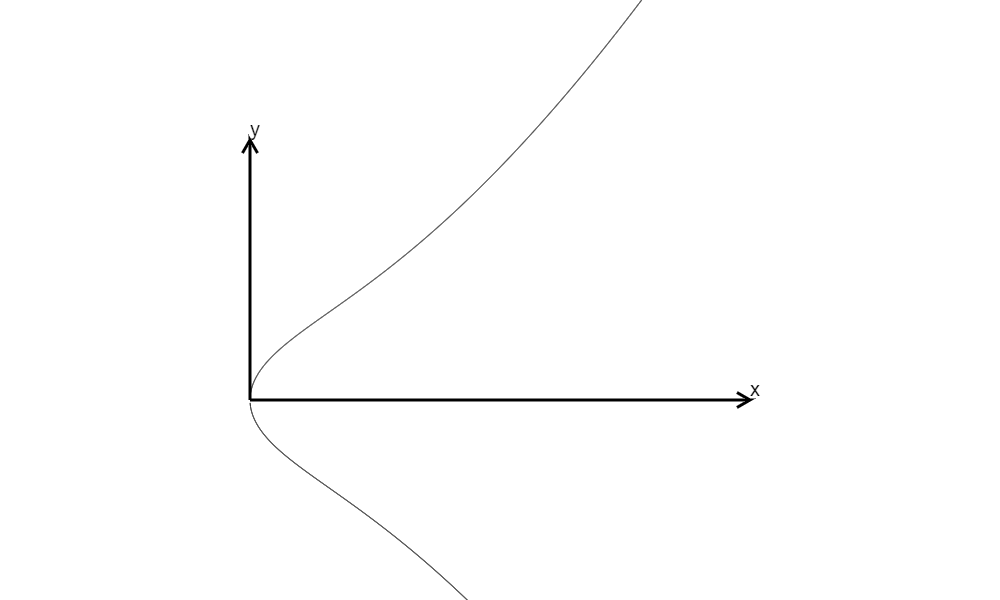\(y^2=x^3+x=x(x^2+1),\Delta=-64\)

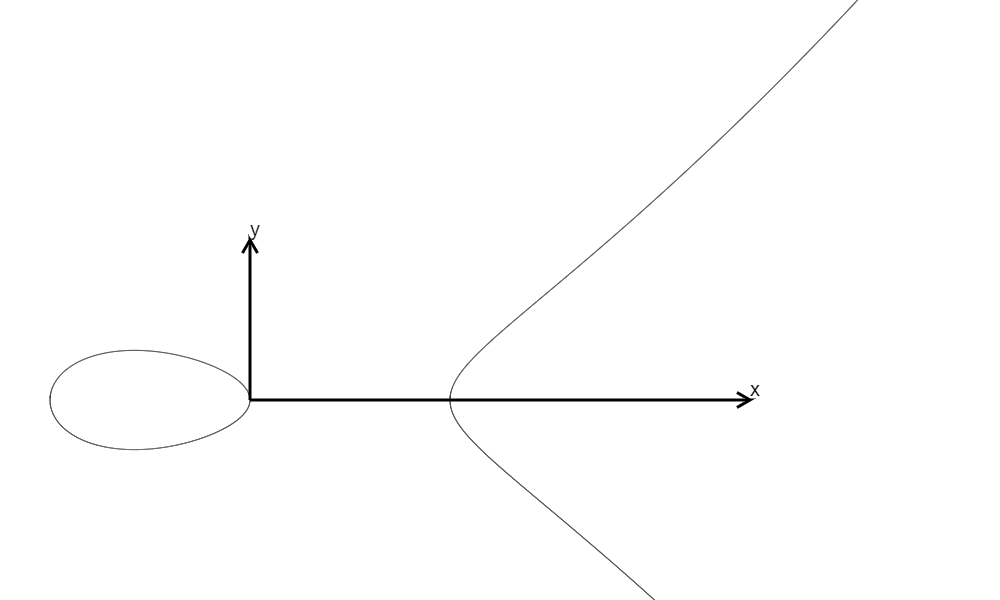\(y^2=x^3-x=(x-1)x(x+1),\Delta=64\)

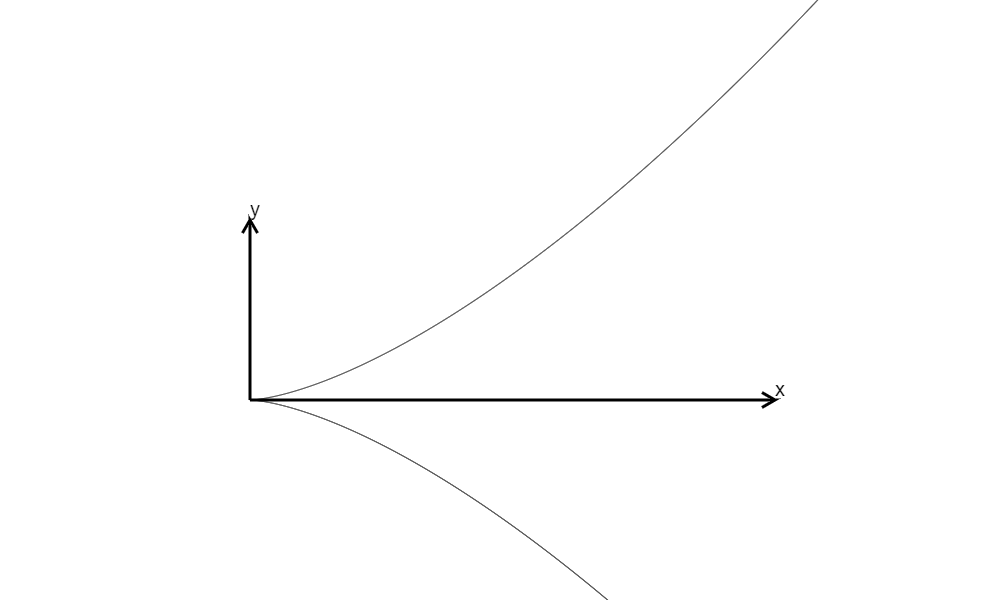\(y^2=x^3,\Delta=0\)

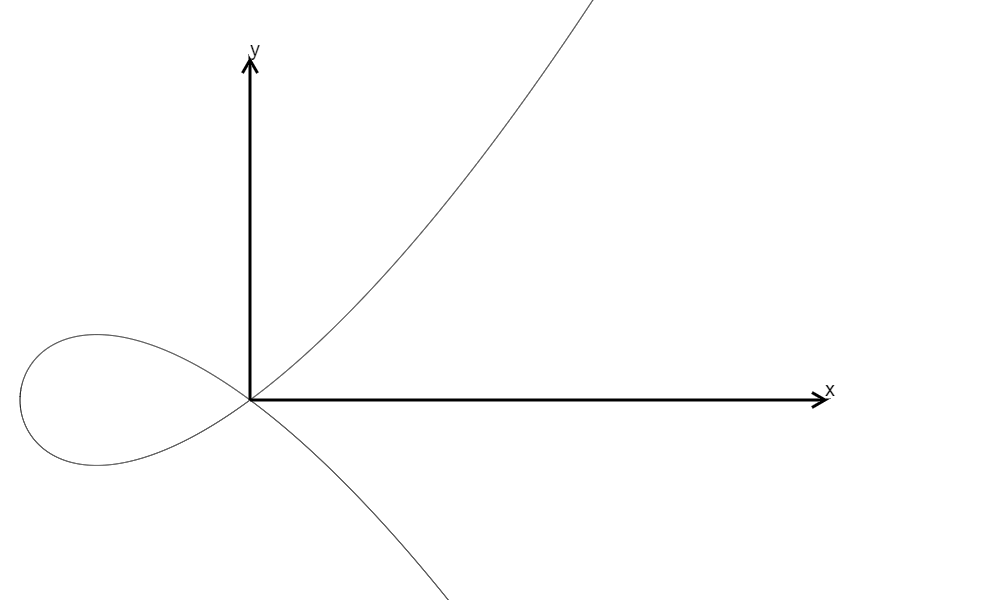\(y^2=x^3+x^2=x^2(x+1),\Delta=0\) (Not in Weierstrass Form)

We also define the quantity \(\Delta\), called the discriminant, as \(\Delta=-16(4A^3+27B^2)\). If \(\Delta\) is non-zero, then we call the curve non-singular, and we will just study non-singular elliptic curves in this post.

We note that this discriminant exactly corresponds with the disriminant of the cubic equation \(x^3+Ax+B=0\), and discriminant being 0 means that the cubic equation only has repeated roots, making the curve “non-differentiable” at some point, so we do not worry about these curves. On the other hand, if the discrimint is positive, then the equation has 3 real roots; and if it is negative, then the equation has 1 real root.

We have the definition of elliptic curve, which is great. But how about the “group law” we are used to hearing for elliptic curve? Indeed if we just look at the curve, it is not apparent that a group law can be defined over an elliptic curve.

Group Law

Take an “differentiable” elliptic curve. Then we can define an “addition” operation of any two points on the curve as follows:

1. Infinity

If one of the points is the point at infinity, WLOG assume \(P=\mathcal{O}\), then \(P+Q=O+\mathcal{O}=Q\). Same for \(Q=\mathcal{O}\).

2. \(P\neq Q\) both not infinity

If we take two points \(P\) and \(Q\) on the curve (for \(P\neq Q\)) and both not infinity, we can draw a line with that two points. Then (just take for granted that) the intersection of that line and the elliptic curve will contain another point \(R\) on the curve (besides \(P\) and \(Q\) already). If it really does not exist (for vertical lines), we can still say that the third point of intersection is \(\mathcal{O}\).

For example if you are considering the point \((x,y)\) and \((x,-y)\), then the straight line will not intersect any other points on the curve, so we say \(\mathcal{O}\) is the third point of intersection.

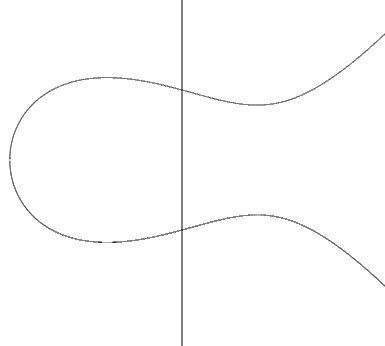
As an example, we consider the curve \[y^2=x^3-x+1\] Let \(P=(0,1)\) and \(Q=(3,5)\). Check to see that \(P\) and \(Q\) are on the curve. Then we can draw a line passing through \(P\) and \(Q\) to find a third point \(R\).

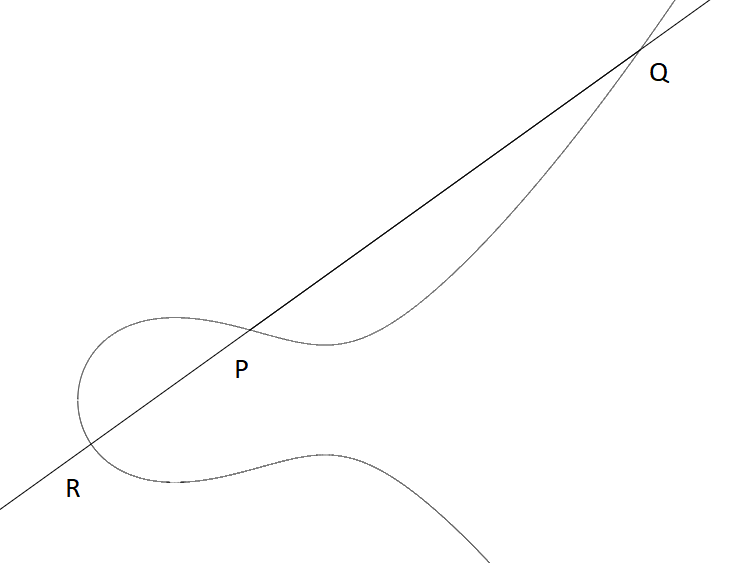
Then, if the coordinate of the third point is \((x,y)\), then \(P+Q\) is defined as the point \((x,\mathbf{-y})\). The geometric meaning is to draw a vertical line on the third point, and the other intersection is what we call \(P+Q\). 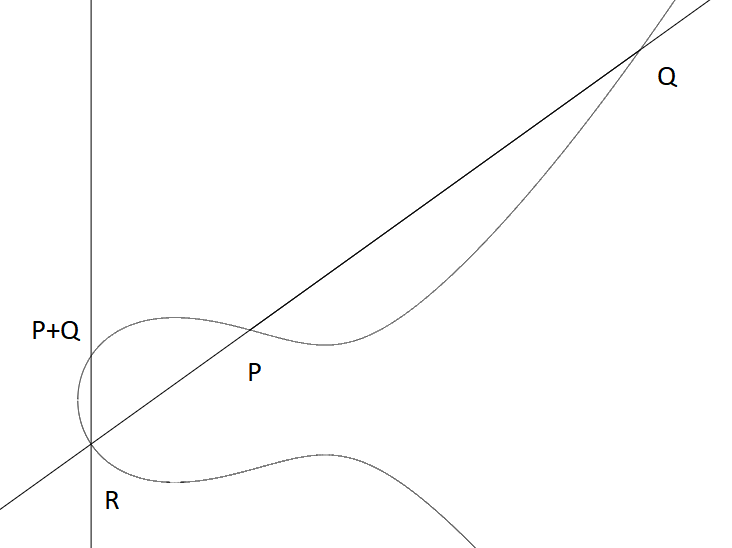In this case, we can do the algebra (or just use the explicit formula) to find that the third point of intersection has coordinate \((-\frac{11}{9},-\frac{17}{27})\), so \(P+Q = (-\frac{11}{9},\frac{17}{27})\).

3. \(P=Q\neq\mathcal{O}\)

What if \(P=Q\)? Then instead of drawing a line that passing through two points, we just draw the tangent of the curve at \(P\). Then the line will intersect the curve at another point again (actually it still has 3 intersections, just one repeated root). Then the procedure is the same as above.

Inverse Element

If we have \(P=(x,y)\), then note that since \((x,y) + (x,-y) = \mathcal{O}\), then the inverse of \(P\) is \((x,-y)\). We can just denote the inverse as \(-P\). Note that this means that if \(P\), \(Q\) and \(R\) are colinear, then \(P+Q+R=\mathcal{O}\).

Group Properties

The operation we defined this way has several properties: For any points \(P,Q,R\in E\) (\(E\) is the elliptic curve),

1. \(P+Q\in E\) (Closure)
2. \(P+\mathcal{O}=\mathcal{O}+P=P\) (identity)
3. \(P+Q=Q+P\) (commutivity)
4. \((P+Q)+R=P+(Q+R)\) (associativity)

The first and second property is trivially true from our construction. The third one is true by the geometric intuition. The fourth property, however, is actually very difficult to prove. While you can use the explicit formula for addition to validate it, but it is very cumbersome. We will just take associativity for granted.

Then the operation we defined make \(E\) into a group!

Explicit Formula for Point Addition

The formula, or actually the algorithm for point addition is as follows: For \(P=(x_1,y_1)\) and \(Q=(x_2,y_2)\) both in the elliptic curve \(E\), if we want to calculate \(P+Q\),

1. If \(P=\mathcal{O}\), then \(P+Q=Q\).
2. If \(Q=\mathcal{O}\), then \(P+Q=P\).
3. If \(x_1=x_2\) and \(y_1=-y_2\), then \(P+Q=\mathcal{O}\).
4. Define \(\lambda\) by \(\displaystyle\lambda=\begin{cases} \frac{y_2-y_1}{x_2-x_1}\text{ If }P\neq Q\\ \frac{3x_1^2+A}{2y_1}\text{ If }P=Q \end{cases}\)

Now let \(x=\lambda^2-x_1-x_2, y=\lambda(x_1-x)-y_1\), we have \(P+Q=(x,y)\).

The only non-obvious part is (4). If \(P\neq Q\), then \(\lambda\) is the slope of the line that passes through \(P\) and \(Q\). If \(P=Q\), then \(\lambda\) is the slope of the tangent of the curve at \(P\), since by implicit differentiation (actually just the formal derivitive)

\[\begin{align*} y^2=&x^3+Ax+B\\ 2y\frac{dy}{dx}=& 3x^2 + A\\ \frac{dy}{dx}=& \frac{3x^2+A}{2y}\\ \left.\frac{dy}{dx}\right\rvert_{P}=& \frac{3x_1^2+A}{2y_1} \end{align*}\]

Now the equation of the line will be \(y = \lambda x + \nu\), where \(\nu = y_1 - \lambda x_1\) is the y-intersect of the line. Now substitute the line equation to the elliptic curve equation to find intersection: \(\begin{align*} (\lambda x + \nu)^2 =& x^3+Ax+B\\ \lambda^2x^2 + 2\lambda\nu x + \nu^2 =& x^3+Ax+B\\ x^3 - \lambda^2 x^2 + (A-2\lambda\nu)x + (B-\nu^2) =& 0 \end{align*}\)

The is a cubic equation, but we do not need to actually solve it, since we already know two of the intersections of the line with the curve, namely \(P\) and \(Q\) by construction! So the above cubic equation have factor \((x-x_1)(x-x_2)\). So we get\[ x^3 - \lambda^2 x^2 + (A-2\lambda\nu)x + (B-\nu^2)=(x-x_1)(x-x_2)(x-x_3) \] Where we use \(x_3\) to denote the unknown intersection. Now compare the \(x^2\) term on both sides: LHS gives \(\lambda^2\), and right hand side gives the negative of sum of \(x_i\)’s, so \(\lambda^2 = - x_1 - x_2 - x_3\). So \(x_3 = \lambda^2 - x_1 - x_2\).

To recover the \(y-\)coordinate, we just substitute the equation back to the line \(y=\lambda x+\nu\), and get \(y_3=\lambda x_3 + \nu\), then expand to get \(y_3 = \lambda x_3 + y_1 - \lambda x_1 = \lambda (x_3-x_1) + y_1\).

Then \(P+Q\) will be this point reflected along the x-axis, so we just get the negative of \(y_3\), and we get our desired \(P+Q=(x_3, \lambda(x_1-x_3)-y_1)\).

Remarks

We note that in the algorithm for point addition, we actually do not use the value of \(B\). This is curious, as if the point we are “adding” in the curve are actually not in the curve by using a different \(B\), the formula is still the same.

Example

We can define an elliptic curve over the rationals (in computers we use rational numbers instead of real numbers as we can’t represent real numbers accurately anyway). Let’s define the curve \(y^2 = x^3-x+1\) as \(E\), and take the points \((0,1)\) and \((3,5)\) on the curve. We can also see the discriminant of \(E\) is \(-368\).

Note that \(P\) is represented as \((0:1:1)\) instead of just \((0,1)\), but we can ignore the third coordinate for now.

Let’s add \(P\) and \(Q\) to verify our above calculation.

Elliptic Curve over \(\mathbb{F}_p\)

So far we are concerned with elliptic curves over the reals. However, in cryptography, we often need to work with elliptic curves over a finite field \(\mathbb{F}_p\) for \(p\) prime. Recall that \(\mathbb{F}_p\) is just the set \(\{0,1,\cdots,p-1\}\) with addition and multiplication done mod \(p\).

We can, of course, define an elliptic curve over \(\mathbb{F}_p\) using the same definition as for the reals, and for the point addition, we use the same formulae, except the division becomes inverse. All the theories of addition and group structure applies.

In the case of \(\mathbb{F}_p\), the elliptic curve only consists of finitely many points, as \(\mathbb{F}_p^2\) only has \(p^2\) points anyway. Moreover, since each \(x\) only corresponds to 2 \(y\) (because any polynomial over degree \(d\) over a field has at most \(d\) solutions), the number of points are at most \(2p+1\).

We have a even better bound of the maximum number of points on the curve over \(\mathbb{F}_p\) (even with \(\mathbb{F}_{p^n}\) for any \(n\) positive integer), and this is called the Hasse’s Theorem: If \(\#E(\mathbb{F}_q)\) is the number of points on an elliptic curve over \(\mathbb{F}_q\) for \(q\) prime or power of primes, then \[ (q-1)-2\sqrt{q}\leq \#E(\mathbb{F}_q)\leq (q-1)+2\sqrt{q}\]

On the other hand, we may also want to know the structure of \(E(\mathbb{F}_p)\). Actually, it is either cyclic, or a product of two cyclic groups, but we will not discuss this here.

Scalar Multiplication

It also makes sense to define the scalar multiple of a point \(P\) to just be adding the point \(P\) to itself a number of times. We use the notation \([n]P = \underbrace{P+\cdots+P}_{n\text{ times}}\) for positive \(n\), and \([n]P = \underbrace{-P-\cdots-P}_{\lvert n\rvert\text{ times}}\) for negative \(n\). We can also say that \([0]P=\mathcal{O}\).

Are there any fast ways to compute \([n]P\)? The naive way is to add \(P\) to itself \(n\) times. But just as the repeated squaring method in modular exponentiation, we can also do this similar approach, and we call this the double-and-add algorithm.

let bits be the bit representation of \(n\)
let \(P\) be the point to be multiplied
let R = \(\mathcal{O}\).
for i from 0 to bits.length():
    \(R = [2]R\)
    if bits[i] == 1:
        \(R = R + P\)
return \(R\)

Order

We may have that \([n]P=\mathcal{O}\) for some positive \(n\). The smallest positive \(n\) such that \([n]P=\mathcal{O}\) is called the order of \(P\). For elliptic curve over finite field, a point will have finite order. If there are no \(n\) such that \([n]P=\mathcal{O}\), then we say the point has infinite order.

If the order of the point is equal to the number of points \(N\) on the curve, this means that \([m]P\) can reach all the points in the curve as \(m\) goes from \(1\) to \(N\), then we call this \(P\) a generator of the elliptic curve. Note that we do not always have one generator, as \(E(\mathbb{F}_p)\) may not be cyclic as mentioned above.

For example, we can use the curve \(y^2=x^3-x+1\) again, and we note that the point \((3,5)\) over the rationals has infinite order. Actually, we can even see that only the point at infinity (represented as \((0:1:0)\)) has finite order (actually order is just 1).

However, over \(\mathbb{F}_7\), we can find that the point \((3,5)\) has order 3.

We can also find that \(E(\mathbb{F}_7)\) has 12 points, is isomorphic to the group \(\mathbb{Z}/12\mathbb{Z}\) (which is cyclic) and that \((5,3)\) is the generator of \(E(\mathbb{F}_7)\) (i.e. has order 12).

Elliptic curves over rationals may still have points of finite order. For example, for the curve \(y^2=x^3+1\), there are 6 points of finite order. The point \((2,-3)\) has order 6. We can verify this by multiplying 6 to the point \((2,-3)\) to get the point at infinity.

Elliptic Curve over \(\mathbb{Q}\)

In fact, a much stronger result is true.

Theorem (Mordell-Weil): For \(K\) a global field, \(E(K)\) is finitely generated.

Let’s specialise to the field of rational numbers \(\mathbb{Q}\), which is indeed a global field, this says that \(E(\mathbb{Q})\) consists of points of finite order (the torsion subgroup), denoted \(E(K)_{\text{tors}}\), and the infinite part will be isomorphic to \(\mathbb{Z}^r\) for some non-negative integer \(r\).

For elliptic curves over \(\mathbb{Q}\), the points of finite order \(P=(x,y)\) will have the following two conditions:

Corollary (Lutz, Nagell):

1. \(x\) and \(y\) are both integers.
2. Either \([2]P=\mathcal{O}\), or \(y^2\) divides \(4A^3+27B^2\).

We have a strong theorem about the torsion subgroup:

Theorem (Mazur):

The structure of the torsion subgroup of elliptic curve over \(\mathbb{Q}\) can only be (isomorphic to) one of the following 15 groups:

1. \(\mathbb{Z}/n\mathbb{Z}\) for \(n=1,2,\cdots,9,10,12\).
2. \(\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2n\mathbb{Z}\) for \(n=1,2,3,4\).

But we shall explore no further in this direction.

Conclusion

This time we have explored the very basic concepts of the elliptic curve, and how a group operation is defined over it. However this still leave some question unanswered.

Actually, what is the point at infinity really doing? It magically makes the elliptic curve into a group, because indeed sometimes you really do not have the third point of intersection of the line and the curve. Is there any geometric meaning?

Why are the points represented as \((x:y:1)\) and infinity as \((0:1:0)\)?

We will answer this question in the next part.

References

Silverman, J. H. (2009). The arithmetic of elliptic curves (Vol. 106, pp. xx+-513). New York: Springer.

1. The correct definition of elliptic curve considers a field \(K\), then define an elliptic curve over \(K\), and consider all the solutions of the curve where the coordinates are in \(\bar{K}\), the algebraic closure of \(K\) (the smallest field containing \(K\) such that it is algebraically closed: every polynomial with coefficients in that field has a root). However we shall not consider this as in the case of \(\mathbb{Z}/p\mathbb{Z}\), we only care about solutions in \(\mathbb{Z}/p\mathbb{Z}\). ↩